Baum–Welch algorithm
In electrical engineering, computer science, statistical computing and bioinformatics, the Baum–Welch algorithm is used to find the unknown parameters of a hidden Markov model (HMM). It makes use of the forward-backward algorithm and is named for Leonard E. Baum and Lloyd R. Welch.
Contents |
Explanation
The Baum–Welch algorithm is a particular case of a generalized expectation-maximization (GEM) algorithm. It can compute maximum likelihood estimates and posterior mode estimates for the parameters (transition and emission probabilities) of an HMM, when given only emissions as training data.
For a given cell 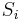 in the transition matrix, all paths to that cell are summed. There is a link (transition from that cell to a cell
in the transition matrix, all paths to that cell are summed. There is a link (transition from that cell to a cell 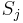 ). The joint probability of
). The joint probability of 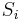 , the link, and
, the link, and 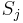 can be calculated and normalized by the probability of the entire string. Call this
can be calculated and normalized by the probability of the entire string. Call this 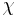 .
.
Now, calculate the probability of all paths with all links emanating from 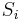 . Normalize this by the probability of the entire string. Call this
. Normalize this by the probability of the entire string. Call this  .
.
Now divide 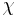 by
by  . This is dividing the expected transition from
. This is dividing the expected transition from 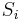 to
to 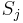 by the expected transitions from
by the expected transitions from 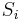 . As the corpus grows, and particular transitions are reinforced, they will increase in value, reaching a local maximum. No way to ascertain a global maximum is known.
. As the corpus grows, and particular transitions are reinforced, they will increase in value, reaching a local maximum. No way to ascertain a global maximum is known.
See also
References
The algorithm was introduced in the paper:
- L. E. Baum, T. Petrie, G. Soules, and N. Weiss, "A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains", Ann. Math. Statist., vol. 41, no. 1, pp. 164–171, 1970.
The Shannon Lecture by Welch, which speaks to how the algorithm can be implemented efficiently:
- Hidden Markov Models and the Baum–Welch Algorithm, IEEE Information Theory Society Newsletter, Dec. 2003.
The path-counting algorithm, an alternative to the Baum–Welch algorithm:
- Comparing and Evaluating HMM Ensemble Training Algorithms Using Train and Test and Condition Number Criteria, Journal of Pattern Analysis and Applications, 2003.
External links
- An Interactive Spreadsheet for Teaching the Forward-Backward Algorithm (spreadsheet and article with step-by-step walkthrough)
- Formal derivation of the Baum-Welch algorithm
- Implementation of the Baum-Welch algorithm